Rediscovering Lagrange Polynomials
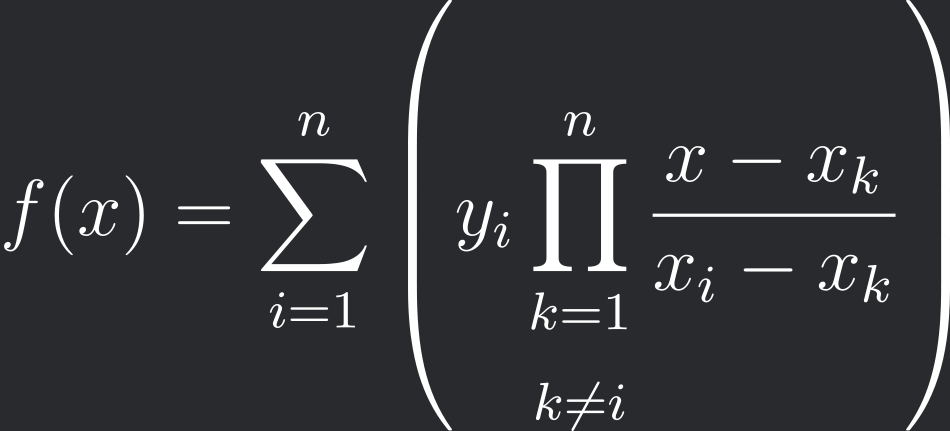
Some time ago, I wanted to find a formula for a function that passes through a given set of points. And since I love reinventing the wheel, I decided to not google the problem and instead find a formula of my own.
Let \(f(x)\) to be the function we are looking for and \(\{(x_{i}, y_{i}) \mid i=1,2,\dots,n \}\) to be the given set of points. My strategy was to express the function as a sum of \(n\) distinct functions \(f_{i}(x)\), each satisfying the properties below. $$ f_{i}(x_{j})=0; i \neq j $$ $$ f_{i}(x_{i})=y_{i} $$
For the sake of simplicity and intuitivity, I’ll change the strategy a bit. Instead, our \(f_{i}(x)\)’s will satisfy these properties; $$ f_{i}(x_{j})=0; i \neq j $$ $$ f_{i}(x_{i})=1 $$ and we are going to write \(f(x)\) as; $$ f(x) = f_{1}(x)y_{1} + f_{2}(x)y_{2} + \dots + f_{n}(x)y_{n} = \sum_{i=1}^{n}f_{i}(x)y_{i} $$
This made things a bit easier to see and better in my opinion. Also, I will call \(f_{i}(x)\)’s as “filters” from now on, as they filter out the unwanted x values. Now let’s think about how we can create such filter functions. I’d suggest you pause reading and think about the problem on your own. I promise, it is pretty easy. First, let’s focus on making the output zero. We are going to use a chain of multiplications. Precisely, \(f_{i}(x)\) will be the product from \(k=1\) to \(n\) (skipping the \(k=i\) term) of \((x-x_{i})\). Let’s write it down in mathematical terms. $$ f_{i}(x) = \prod_{\substack{k=1 \\ k \neq i}}^{n}(x-x_{k}) $$
This is not entirely correct though, as we don’t know what it outputs for \(x=x_{i}\). But we can force it to output \(1\) by dividing each term by \((x_{i}-x_{k})\). This does not affect the outputs on other \(x\) values since dividing zero by a non-zero number yields zero, but it forces our filter to output \(1\) on \(x_{i}\). So the final form of our filters is going to look like this; $$ f_{i}(x)=\prod_{\substack{k=1 \\ i \neq k}}^{n}\frac{x-x_{k}}{x_{i}-x_{k}} $$
If you recall, to get \(f(x)\) we have to multiply each one of our filters with the corresponding output value and take their sum. $$ f(x)=\sum_{i=1}^{n}f_{i}(x)y_{i} $$ Written explicitly; $$ f(x)=\sum_{i=1}^{n} \left(y_{i}\prod_{\substack{k=1 \\ k \neq i}}^{n} \frac{x-x_{k}}{x_{i}-x_{k}} \right) $$
And we are pretty much done, we got to the Lagrange Polynomials. Although, this was not the formula I had ended up with when I was first dabbling with this problem. It had an extra product that let me control the degree of the resulting polynomial. $$ f(x)=\sum_{i=1}^{n} \left(y_{i} (x-x_{i}+1)^{\alpha} \prod_{\substack{k=1 \\ k \neq i}}^{n} \frac{x-x_{k}}{x_{i}-x_{k}} \right) $$ The positive values of \(\alpha\) allow you to safely increase the degree of the resulting polynomial while guaranteeing for it to pass the given points. Sadly for negative values of \(\alpha\) it does not behave this way. And the positive values of \(\alpha\) are not that useful as well, since you’d generally want to have the most simplified polynomial.
Lastly, here’s a python program that computes the polynomial using the Sympy library.
from sympy import Symbol, Expr, simplify
from typing import Iterable
def filtered_product(expr: Expr, x: Symbol, iterable: Iterable, value_to_ignore):
p = 1
for i in iterable:
if i == value_to_ignore:
continue
p *= expr.subs(x, i)
return p
def make_filter(inputs: list, i, x: Symbol) -> Expr:
x_k = Symbol('x_k')
return filtered_product((x-x_k)/(i-x_k), x_k, inputs, i)
def generate_polynomial(inputs: list, outputs: list, x: Symbol, simplify_output: bool=True):
final_expr = 0
for i, inp in enumerate(inputs):
final_expr += outputs[i] * make_filter(inputs, inp, x)
if simplify_output:
final_expr = simplify(final_expr)
return final_expr
def main():
x = Symbol('x')
# You can modify those however you want
inputs = [1, 2, 3]
outputs = [4, 5, 6]
prod = generate_polynomial(inputs, outputs, x)
print(prod)
while True:
try:
val = int(input('> '))
print(prod.subs(x, val))
except KeyboardInterrupt:
break
if __name__ == "__main__":
main()
Bonus
Before writing this post, I tried to solve it in a different way, I wanted to have \(n\) filters, when multiplied give the desired function. Let’s denote them with \(g_{i}(x)\). Our desired function \(f(x)\) becomes; $$ f(x)=\prod_{i=1}^{n}g_{i}(x) $$
Similarly, our filters should satisfy equations; $$ g_{i}(x_{j})=1; i \neq j $$ $$ g_{i}(x_{i})=y_{i} $$
Finding these filters is much harder task, but I went with the lazy approach and wrote our new filters in terms of the old ones. $$ g_{i}(x) = (1-f_{i}(x)) + f_{i}(x)y_{i} = 1 + (y_{i} - 1)f_{i}(x)$$
I won’t write formula explicitly here, but here’s a short python snippet that generates the polynomials by that formula.
def generate_polynomial_prod(inputs: list, outputs: list, x: Symbol, simplify_output: bool=True):
final_expr = 1
for i, inp in enumerate(inputs):
final_expr *= 1 + (outputs[i] - 1) * make_filter(inputs, inp, x)
if simplify_output:
final_expr = simplify(final_expr)
return final_expr
As you might guess, the degree of this polynomial grows pretty fast with respect to the input size. So it is not really applicable to any real world situation. But it is still a cool way to express the desired polynomial, so I wanted to include it in.